USANDO A FÓRMULA DE BASKARA

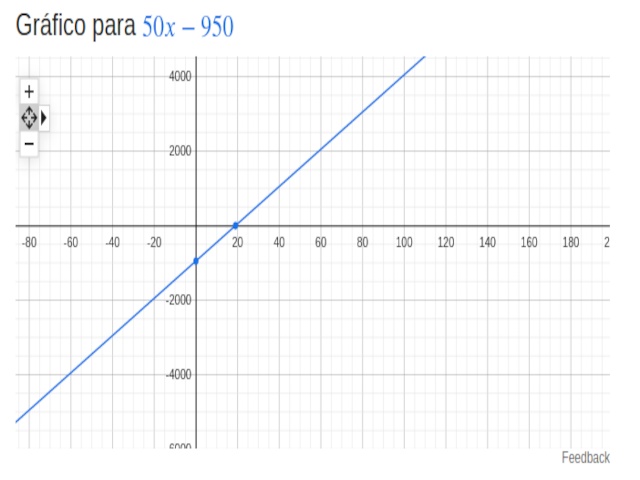
Conforme demonstrado na imagem, o gráfico de uma função quadrática tem formato de uma parábola com cavidade voltada para cima se o elemento “a” da equação for maior que zero e cavidade voltada para baixo se o elemento “a” da equação for menor que zero, Sendo este gráfico, resultado de uma equação quadrática, equação de segundo grau.

A fórmula resolutiva para equações quadráticas do tipo ax² + bx + c = 0, recebe o nome de fórmula de Bhaskara em homenagem ao matemático, professor, astrólogo e astrônomo indiano Bhaskara Akaria, considerado o mais importante matemático do século XII e o último matemático medieval de grande destaque na índia.

O gráfico acima é resultado da seguinte equação:

-x² + 6x -5 = 0

onde:

a = -1

b = 6

c = -5

Para montar o gráfico são necessários quatro pontos no plano cartesiano que podem ser obtidos com os seguintes passos:

Seguindo a fórmula de Bhaskara temos:

Δ = b²–4.a.c

Δ = -1²–4.(-1).(-5)

Δ = 16

Para x podemos ter até dois valores dados pela seguinte operação:

Ou seja

X1 = (-6 + 4) : -2

x1 = -2 : -2

x1 = 1

x2 = (-6 - 4) : -2

x2 = -10 : -2

x2 = 5

Com isso temos os pontos do gráfico que interceptam o eixo x no plano cartesiano, no caso 1 e 5, e sabemos que o eixo y é interceptado no valor de “c”, ou seja em -5. Resta agora encontrar o quarto ponto, o vértice da parábola, resultado da intersecção entre outros dois pontos conhecidos como Xv(x do vértice), pois tem sua localização no eixo x e Yv(y do vértice), pois tem sua localização do eixo y. Para tanto basta usar as seguintes fórmulas:

Encontrando o Xv:

Xv = -b / (2.a)

Xv = -6 / (2.-1)

Xv = -6 / -2

Xv = 3

Uma outra forma de encontrar o Xv é calcular a média aritmética entre as duas raízes de x, exemplo:

Xv = (1+5)/3

Xv = 3

Encontrando o Yv:

Yv = -Δ / (4.a)

Yv = -16 / (4.-1)

Yv = -16 / -4

Yv = 4

logo, vértice = (3, 4)

Agora tempos os quatro pontos necessários para desenhar a parábola do gráfico, são eles:

c = -5

x1 = 1

x2 = 5

V = (3, 4)

Basta localizar os pontos e traçar o gráfico pare termos o resultado esboçado na imagem acima.

Com base no exemplo dado podemos perceber que temos três variáveis a serem lidas em nosso algoritmo: “a”, “b” e “c” e cinco fórmulas a serem implementadas. Sendo assim é necessário fazer a leitura dessas variáveis para que elas possam ser submetidas a fórmula de Bhaskara e demais fórmulas. Com isso, temos o seguinte algoritmo:

Cabe destacar que os comandos “escreva” e “escrevaln” produzem saída de dados, o primeiro sem quebra de linha e o segundo com quebra de linha. O comando “leia” e leitura/entrada de dados. O símbolo asterisco(*) é usado para multiplicação e barra(/) para divisão.

Já com relação ao processamento de dados temos as seguintes fórmulas para encontrar os valores de x1 e x2:

• $x1 = (-$b + sqrt(pow($b,2)-4*$a*$c))/(2*$a); // Bhaskara para x1

• $x2 = (-$b – sqrt(pow($b,2)-4*$a*$c))/(2*$a); // Bhaskara para x2

• $xv = -$b / (2 * $a); // fórmula para encontrar o x do vértice

• $delta = pow($b,2) - (4 * $a * $c); // fórmula para encontrar o delta

• $yv = -$delta / (4 * $a); fórmula para encontrar o y do vértice

Onde “sqrt” é uma função para calcular raiz quadrada e “pow” é uma função para calcular potenciação, considerando que, na maioria das linguagens de programação, funções destinas a esse fim recebem esses nomes.

Com isso temos uma informação matemática transformada em uma informação automática por meio de um algoritmo.

ATIVIDADES

1) Implemente o algoritmo que gera os pontos do gráfico de uma função quadrática no interpretador de algoritmos disponível em http://www.rmfais.com/phpalgor

2) Usando o algoritmo que gera pontos necessários, monte o gráfico das seguintes equações:

a) x² – 4x +3 = 0;

b) x² – 2x -3 = 0;

c) x² + 4x -3 = 0;