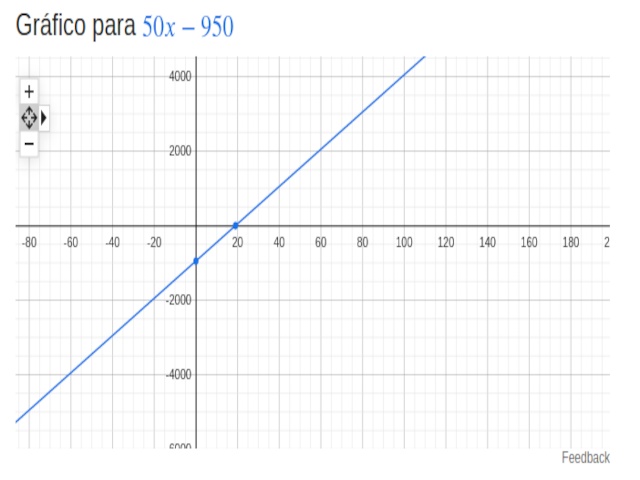
Conforme demonstrado na imagem, o gráfico de uma função quadrática tem formato de uma parábola com cavidade voltada para cima se o elemento “a” da equação for maior que zero e cavidade voltada para baixo se o elemento “a” da equação for menor que zero, Sendo este gráfico, resultado de uma equação quadrática, equação de segundo grau.

A fórmula resolutiva para equações quadráticas do tipo ax² + bx + c = 0, recebe o nome de fórmula de Bhaskara em homenagem ao matemático, professor, astrólogo e astrônomo indiano Bhaskara Akaria, considerado o mais importante matemático do século XII e o último matemático medieval de grande destaque na índia.

O gráfico acima é resultado da seguinte equação:

-x² + 6x -5 = 0

onde:

a = -1

b = 6

c = -5

Para montar o gráfico são necessários quatro pontos no plano cartesiano que podem ser obtidos com os seguintes passos:

Seguindo a fórmula de Bhaskara temos:

Δ = b²–4.a.c

Δ = 6²–4.(-1).(-5)

Δ = 16

Para x podemos ter até dois valores dados pela seguinte operação:

Ou seja

X1 = (-6 + 4) : -2

x1 = -2 : -2

x1 = 1

x2 = (-6 - 4) : -2

x2 = -10 : -2

x2 = 5

Com isso temos os pontos do gráfico que interceptam o eixo x no plano cartesiano, no caso 1 e 5, e sabemos que o eixo y é interceptado no valor de “c”, ou seja em -5. Resta agora encontrar o quarto ponto, o vértice da parábola, resultado da intersecção entre outros dois pontos conhecidos como Xv(x do vértice), pois tem sua localização no eixo x e Yv(y do vértice), pois tem sua localização do eixo y. Para tanto basta usar as seguintes fórmulas:

Encontrando o Xv:

Xv = -b / (2.a)

Xv = -6 / (2.-1)

Xv = -6 / -2

Xv = 3

Uma outra forma de encontrar o Xv é calcular a média aritmética entre as duas raízes de x, exemplo:

Xv = (1+5)/2

Xv = 3

Encontrando o Yv:

Yv = -Δ / (4.a)

Yv = -16 / (4.-1)

Yv = -16 / -4

Yv = 4

logo, vértice = (3, 4)

Agora tempos os quatro pontos necessários para desenhar a parábola do gráfico, são eles:

c = -5

x1 = 1

x2 = 5

V = (3, 4)

Para concluir, basta localizar os pontos e traçar o gráfico para termos o resultado esboçado na imagem acima.

ATIVIDADE

Monte o gráfico das seguintes equações:

a) x² – 4x +3 = 0;

b) x² – 2x -3 = 0;

c) x² + 4x -3 = 0;